CONTRIBUTOR: Dr. Mavis Kelley, mkelley@ badlands.nodak.edu
Materials: Poster board for each student (or pairs); 8 colors of 9×12 construction paper, cut into strips for each student (1 of each color – extra for practicing); glue; markers; ruler; plastic cars or trucks;
Fractional Concepts: Continuous Fractions (partitioned wholes); Fraction Sense; Addition and Subtraction of Fractions; Equivalent Fractions Procedure
1. Have the students practice folding paper strips into equal parts. Thirds, sixths, ninths, and twelfths are more difficult for children to fold. Discuss how many parts/folds are in each strip and how the fractions are named.
2. Mark the large piece of construction paper with a vertical line about 2 cm from the left margin.
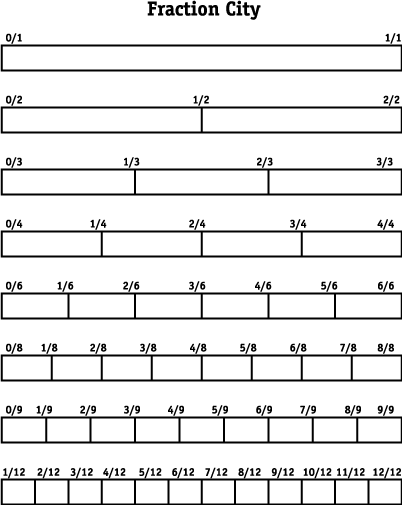
3. Glue on unfolded strip (one whole) lengthwise on the sheet by placing it flush against the line. This is First Street. (One whole=First Street).
4. Show the students how to fold a strip into two equal parts by working with the fold until the strip lies flat. Darken the crease with a pencil or thin marker.
5. Place this strip below the first one, leaving 2-3 cm between the strips.
6. Do not glue the strips until they are all done. That way the strips can still be moved.
7. Work with the students to fold another strip in half and then in half again. Open the strip and fold it back and forth so it will stay flat. Darken the folds and place this strip 2-3 cm below the second strip. Continue the same process for eighths.
8. Help children fold another strip in thirds. Take the time needed to make the folds as accurate as possible. You can use a ruler. Prepare this strip as before and place it on the large sheet, leaving about 2-3 cm space between all the strips.
9. Fold the next strip in thirds and then in half to get sixths. Prepare and position the strip in the same manner as previously described. Discuss how the same result can be obtained by folding a strip in half and then by folding those sections into thirds. Have the children try it. Continue for ninths and twelfths.
10. Throughout the process, ask the students to look for patterns. How many folds does a strip have? How many parts? Use this discussion to rearrange the strips so that the strip with 2 parts is followed by the strips with 3 parts, 4 parts, etc. Glue the strips to the poster board.
11. With older students, make the connection to multiplying fractions while folding. Example: if you are folding the fourth strip, you fold in half and half again. 1/2 of 1/2 is 1/4.
12. Each strip of paper is a street and all streets are the same length.
13. Each part of a street is a block, and all the blocks on one street are the same length. Therefore, First Street has one block, Second Street has two blocks, and so on.
14. Have the children drive their cars on a street. Help them discuss on which street they are located and how many blocks they have driven. Help them to become aware that there is a different name for the total distance on each street because each street has a different number of blocks.
15. Talk about how hard it is to tell where they are at without the strteets being labeled. Lead them into identifying their location by street signs in which the bottom number tells how many blocks a street has, and the top number tells how many blocks on that street their car has driven.
1 The number of blocks driven
2 The number of blocks on the street
16. Have the students put the street signs on all the blocks on their map of Fraction City.
17. Use the Fraction City map for teaching the following concepts:
Comparing Fractions – Have the students use 2-3 toy cars to drive in Fraction City. Ask them to drive two blocks on Third Street and park. Ask them to drive another car two blocks on Fourth Street and park. Encourage them to discuss how far the two cars are from the beginning of each street. Encourage them to explore the fact that even though each car traveled two blocks, the cars did not travel the same distance. Discuss the same number of blocks on other streets. Encourage further exploration and discussion.
Equivalent Fractions – Drive 1 block on Second Street. Drive 2 blocks on Fourth Street. What do you notice?
Addition of Fractions of Like and Unlike Denominators –
Travel 4 blocks on Sixth Street; travel 2 more blocks on Sixth Street. How far have you traveled? Make up additional problems such as this. 4/6 = 2/6 = 6/6 (you went the entire street)
Travel one block on Third Street. Travel one block on Fourth Street. How could you determine the distance traveled? (Find the block with equivalent fractions.)
Subtraction of Fractions – Travel three blocks on Ninth Street. Go back one block. How far have you traveled?
18. When ready, students can write number sentences to describe their movement on their Fraction City map.
19. To explore mixed numerals, place two Fraction Cities together.